Публикувал: Никола Бенин
Днес ще се потопим малко дълбоко в известната техника за намаляване на размерите, наречена Анализ на главните компоненти (PCA).
Първо, нека видим често срещания начин за извършване на PCA с помощта на eigendecomposition.
Да започнем с определяне матрица данни X . Размерът на X е „ n“ от „ f“ . Може да си помислите, че матрицата с данни има „ n“ брой проби и „ f“ брой функции.
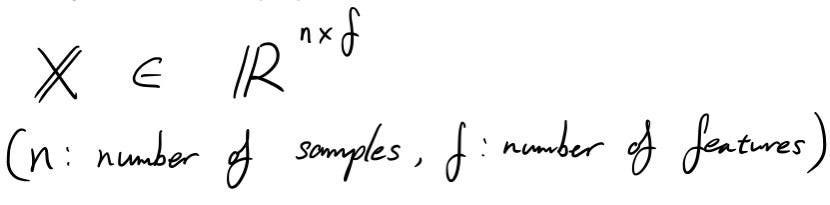
Преди да стартирате PCA, винаги е по-добре да центрирате данните, защото в крайна сметка PCA просто върти данните наоколо, за да проектира данните върху основните компоненти.
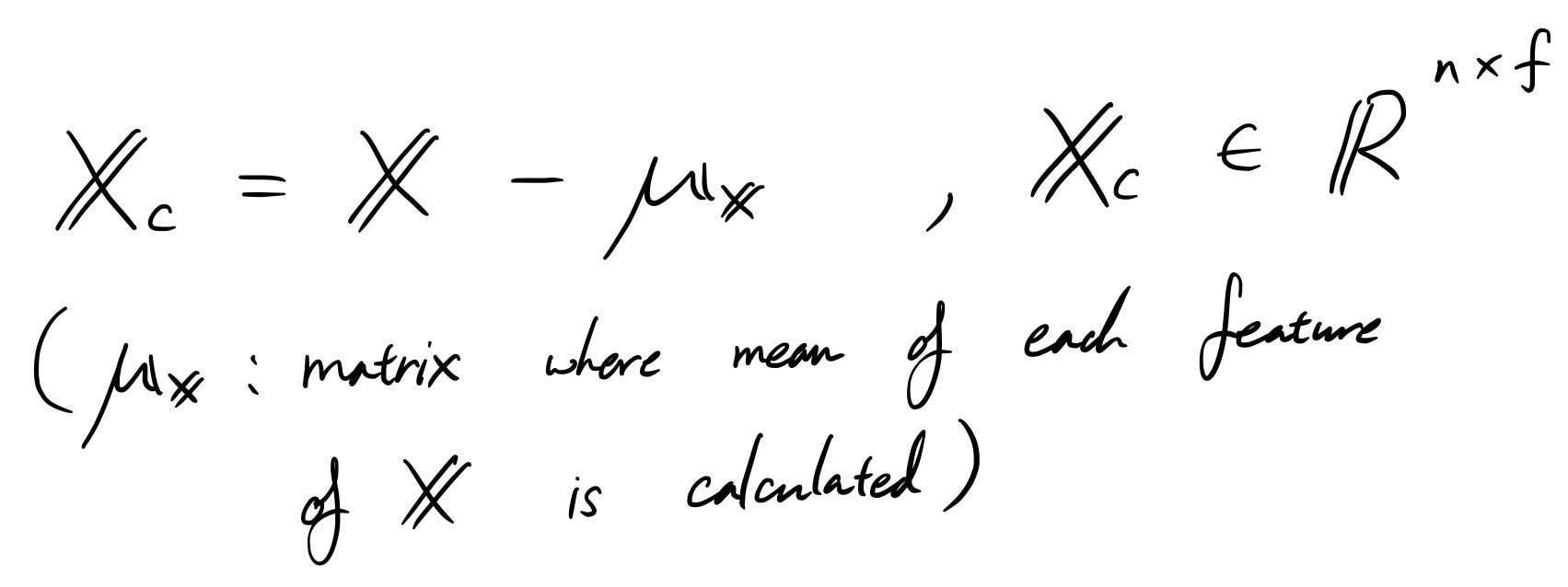
Разбира се, ние извадихме само средното от всяка колона с характеристики, така че измерението не се е променило.
Сега, ако прочетете как да изчислите PCA, една от често срещаните стъпки, които виждате, е да изчислите примерната ковариационна матрица, използвайки центрираните данни.

И вие изпълнявате или разлагане на eigendecomposition, или разлагане на единична стойност (ще обясня тази версия в по-късната част на историята).
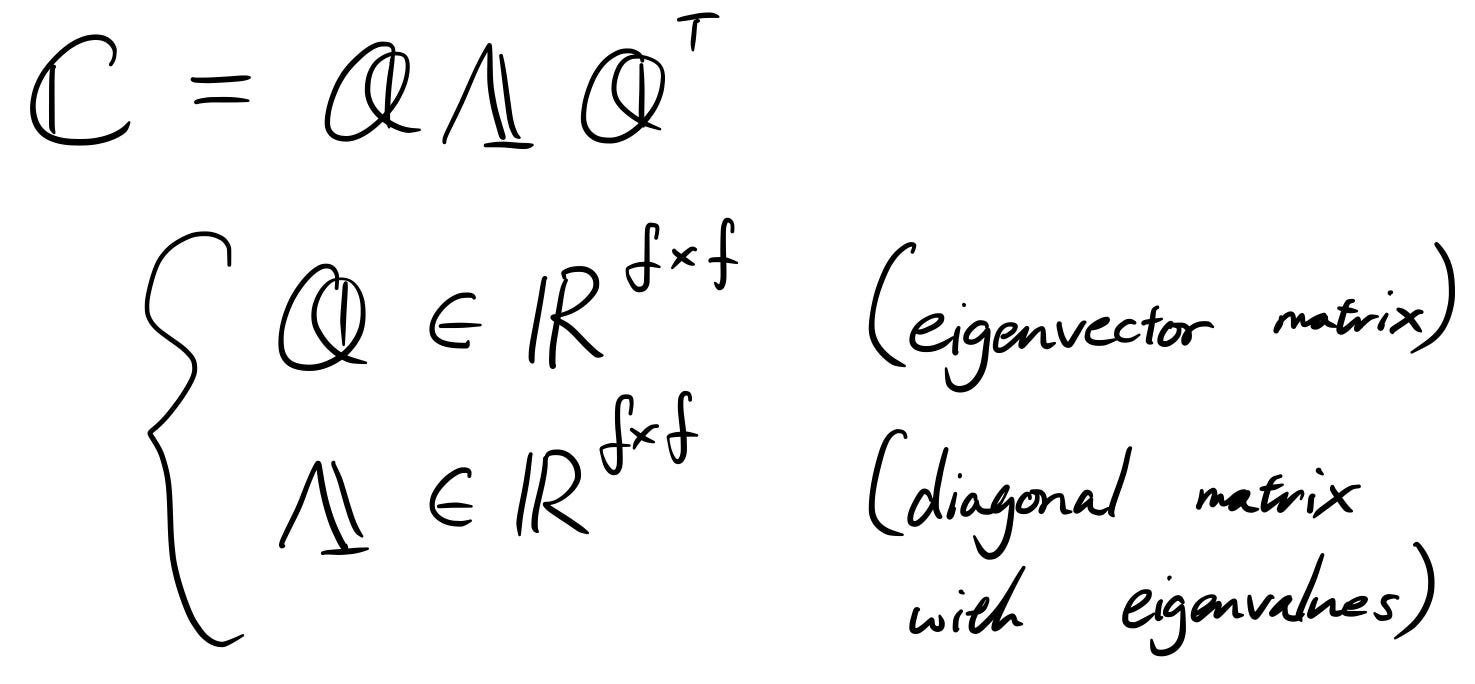
Накратко, собствената матрица Q е матрицата, която съдържа основни компоненти, а Λ е матрицата на собствените стойности (собствени стойности, съответстващи на величината на персоналните компютри, така че можете да ги подредите от големи към малки, така че колкото по-голяма е собствената стойност, толкова по-важно е съответното Компютър е).
Така че, за да намалите размерността, просто бихте избрали няколко основни компонента, да кажем „ s“ от тях. Сега сте избрали номера на матрицата на основните компоненти Q_s .
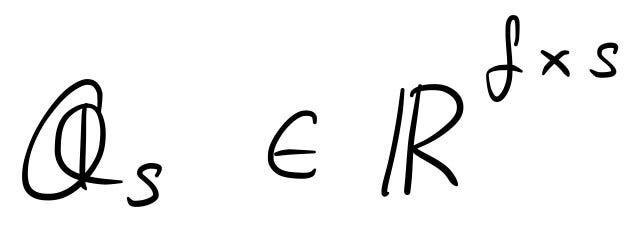
В крайна сметка, ако искате да проектирате оригиналната матрица с данни върху осите на основния компонент, просто ще умножите матрицата на данните с горната матрица на основния компонент, за да получите следното.

Това е! Лесно!
Чакай малко ...
Да, изчисляването на PCA или прилагането на PCA сами не е толкова трудно. Но винаги се чудех как:
“Максимизиране на дисперсията по основните компоненти”
съответства на
„Извършване на собствено разлагане на ковариационната матрица“
Очевидно има по-малко статии, обясняващи това. Един от малкото, които намерих, са връзките, които публикувах по-рано и нека да го обясня тук.
Да предположим, че имате главен компонент вектор v .
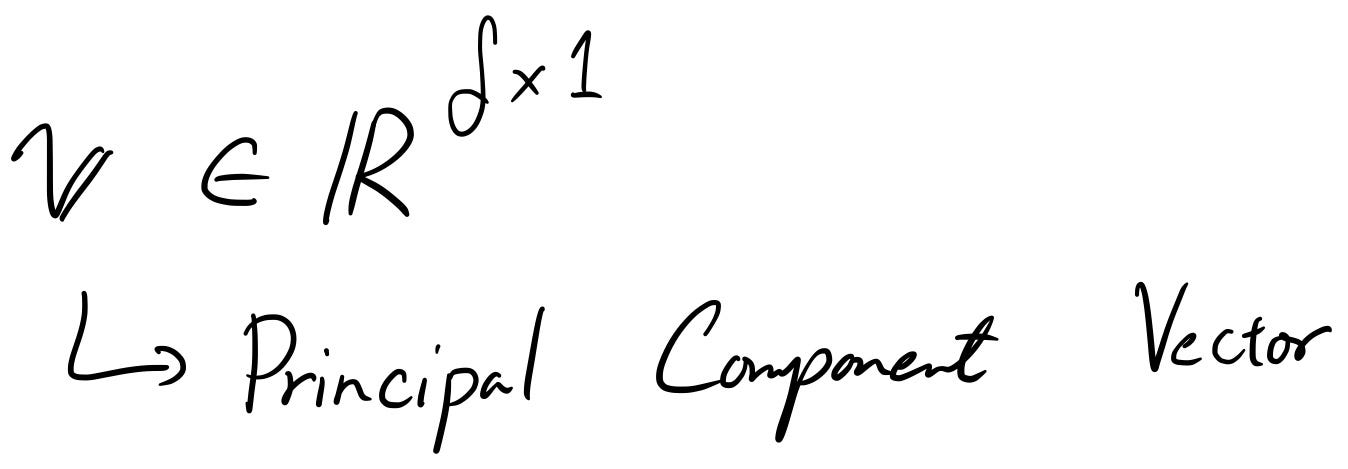
Сега нека използваме това, за да проектираме данните на компютъра.
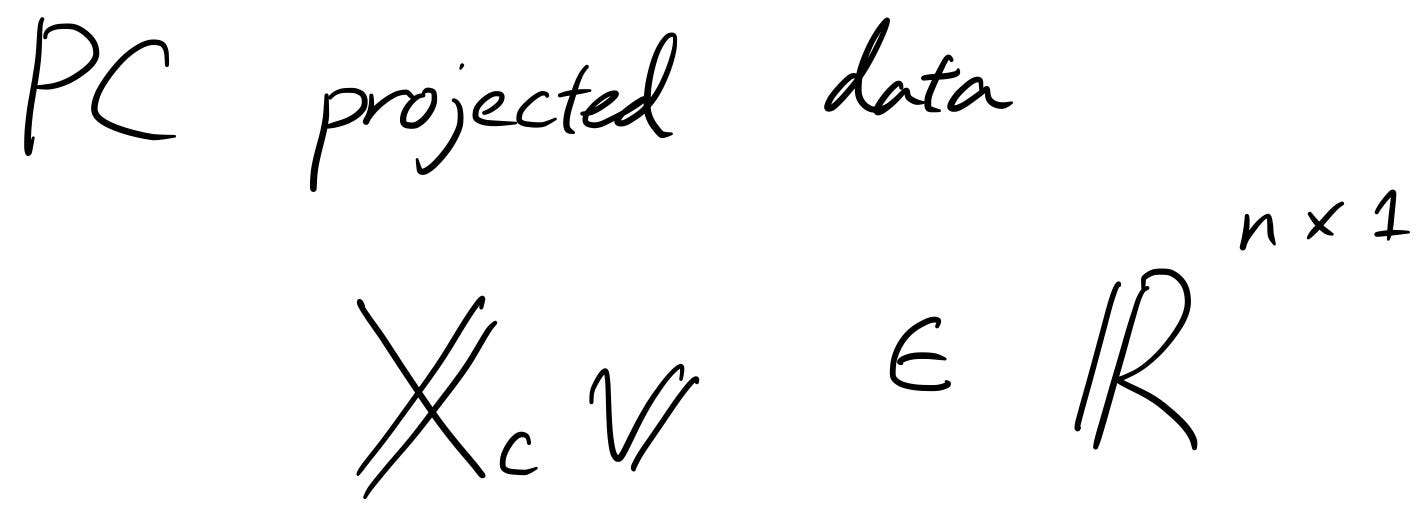
Ако това са прогнозните данни, дисперсията трябва да бъде увеличена, нали? Защото това беше целият смисъл на PCA.
Така че първо, нека изчислим дисперсията на пробата.
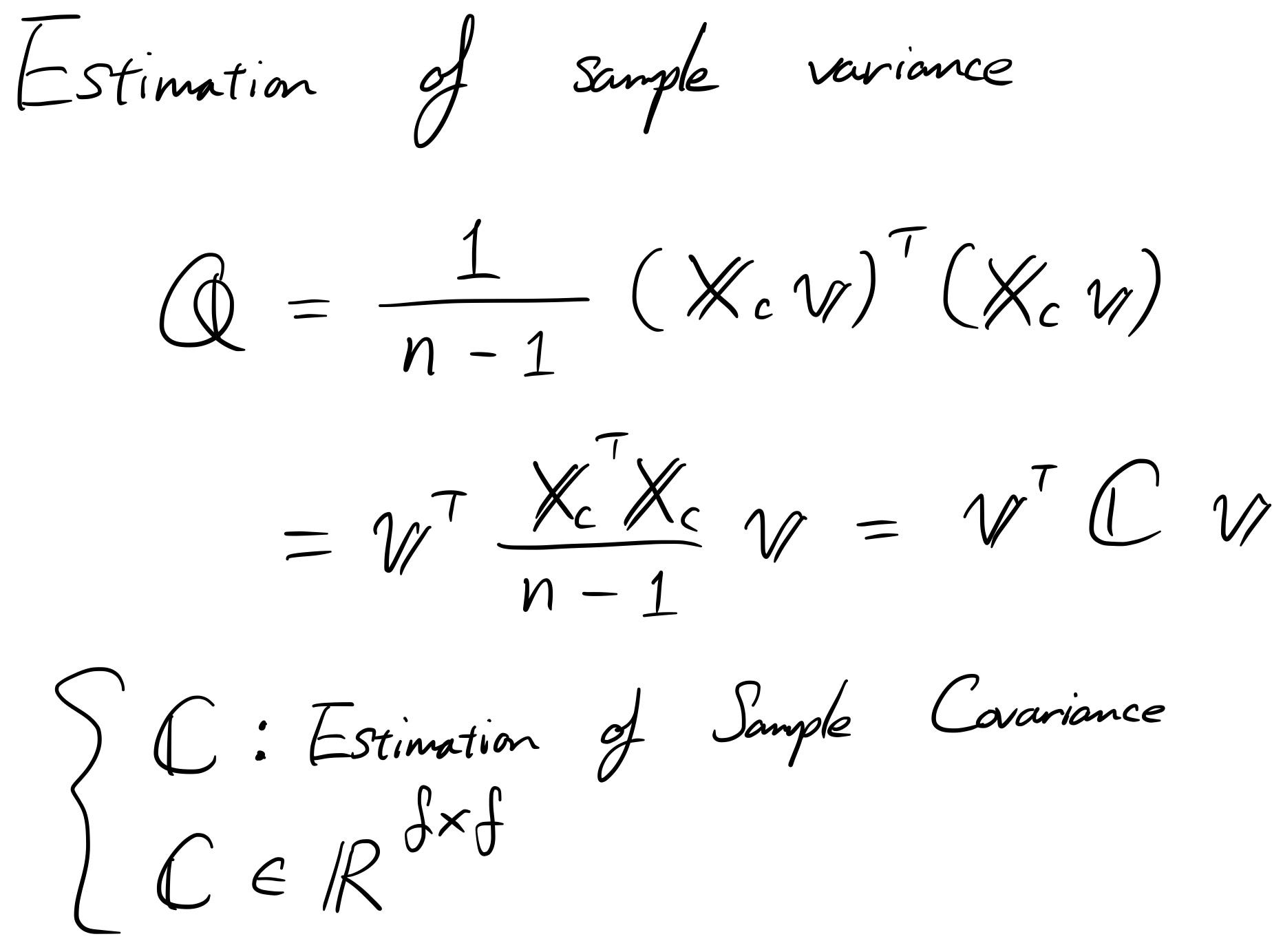
Тъй като цялостната цел на PCA е да максимизира дисперсията по проектираната ос, ще направим това и в уравнението. Но трябва да внимаваме. Ако не зададем ограниченията, да речем имаме много голямо „ v “, тогава лесно можем да увеличим дисперсията „Q“. За да избегнем това, ние задаваме ограничение, за да го направим еднороден вектор.
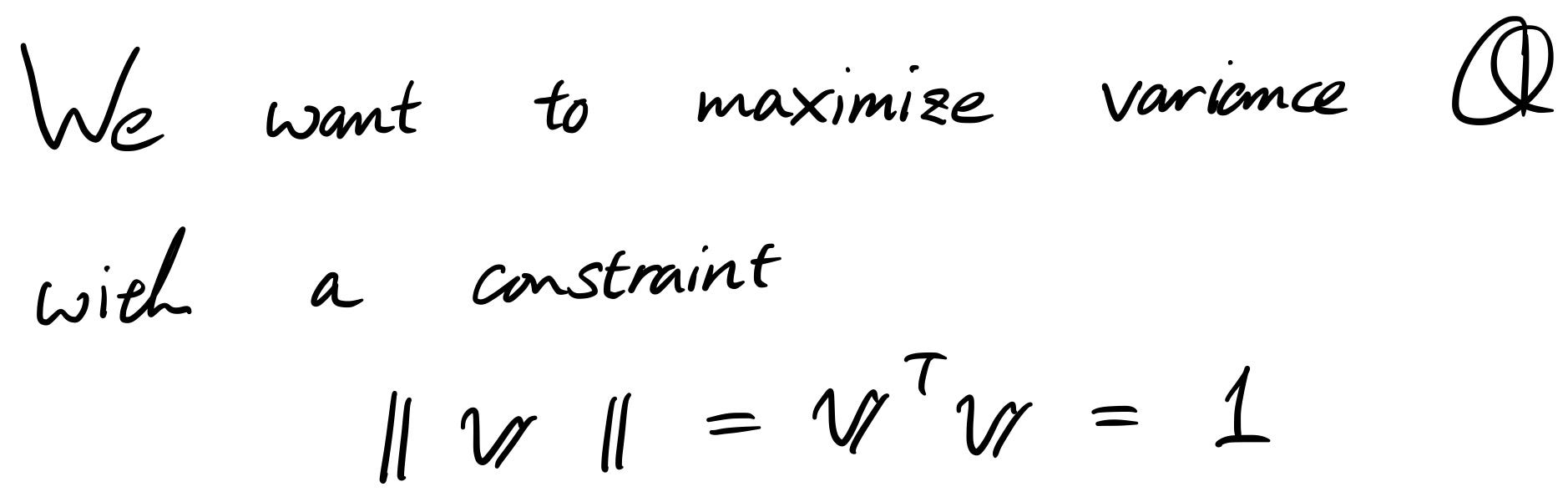
Сега имаме проблем.
- Искаме да увеличим максимално „Q“
- Но в същото време сме ограничени от „ v “
За да разрешат този вид проблеми, хората обикновено използват множител на Лагранж.
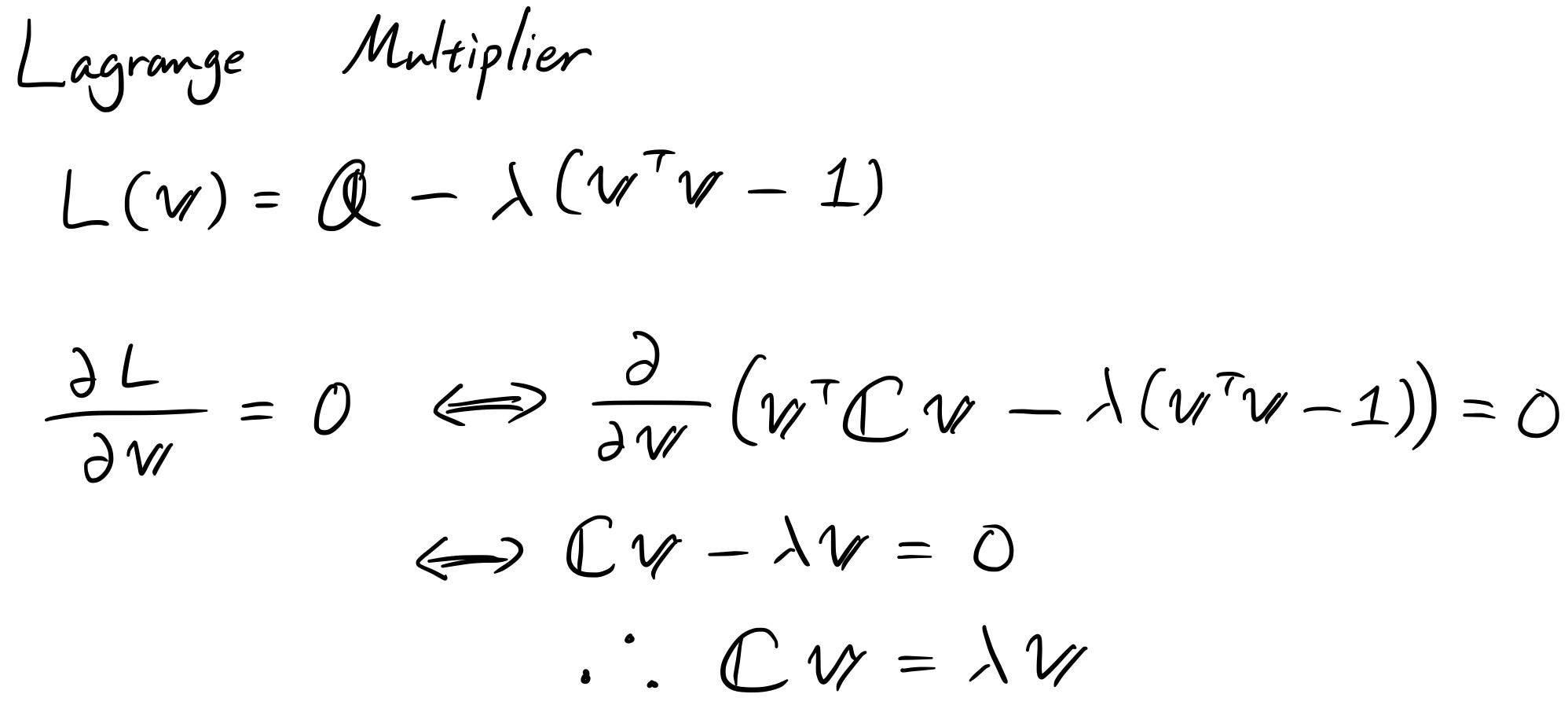
(Имайте предвид, че за да бъдете по-точни, трябва да проверите и други производни, но ние просто игнорираме тези тук.)
След решаването на множителя на Лагранж, за да се увеличи максимално дисперсията, векторът “ v ” трябва да бъде собственият вектор на ковариационната матрица! Оттук идва идеята за решаване на собственото разлагане. Ето защо можете да решите PCA, без да правите итеративна оптимизация.
Добре, така че накрая, каква е разликата между PCA, базирана на eigendecomposition, и PCA, базирана на сингуларна декомпозиция (SVD)?
Eigendecomposition PCA беше лесен за разбиране. Както за доказателство, така и за решаване на самия PCA.
На практика обаче по-голямата част от изпълнението се основава на декомпозиция на единична стойност (SVD). Защо така?
Ако си спомняте как изчислихме собствени вектори и собствени стойности, PCA, базиран на собствено разлагане, трябва първо да изчисли ковариантната матрица. Матрицата на ковариацията беше „ f “ от „ f “. Ако „ f “ е малко, това няма да е проблем. Но представете си огромно „ f “, да речем, че имате работа с изображение. „ F “ изведнъж се превръща в огромен брой, в някои случаи над милион. Тогава изчисляването на ковариацията става невъзможно. Тук PCA, базиран на SVD, може да помогне.
Да видим защо.
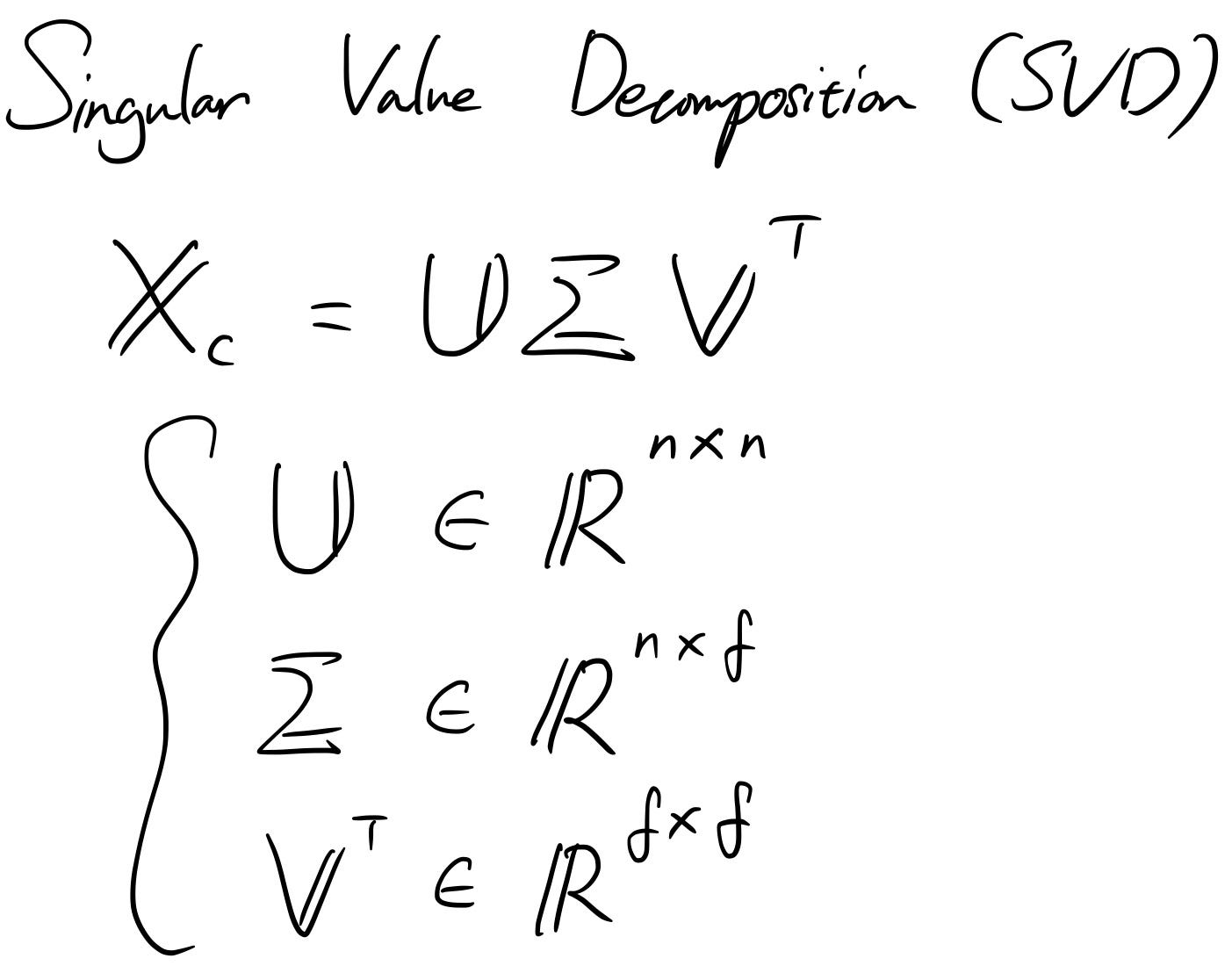
Ако си спомняте SVD, който покрихме миналия път, центрираните данни могат да бъдат декомпозирани в три различни матрици. „ U “ и „ V “ са единични матрици, а „ Σ “ е диагонална правоъгълна матрица.
Нека да видим какво ще се случи, ако следваме същата логика, каквато сме направили при собственото разлагане.
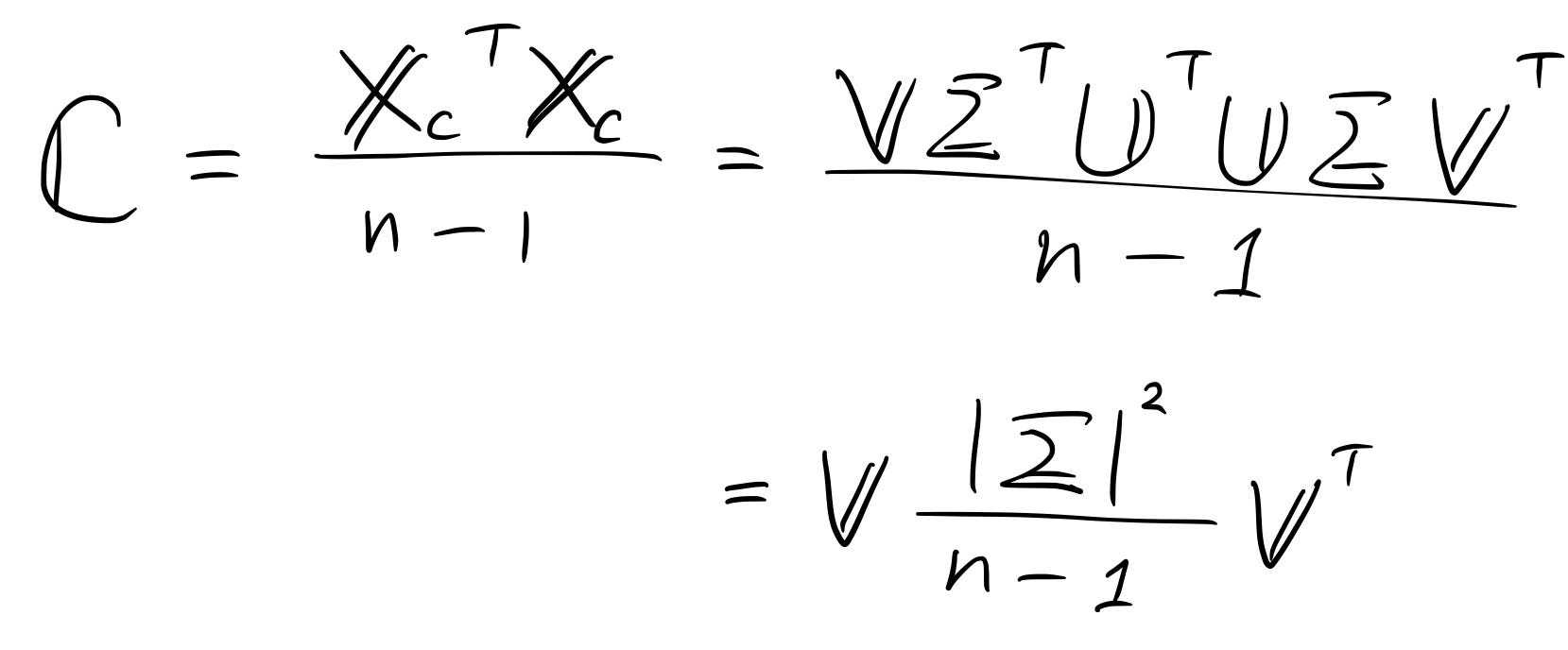
Оказва се, че матрицата " V " е собствената матрица, от която се нуждаехме! Следователно, ако трябва да направим същото и да проектираме данните върху основните компоненти, можем напълно да пропуснем изчисляването на ковариационната матрица, защото следващото уравнение е само измененото уравнение на SVD на центрираната матрица от данни! (Просто трябва да умножите матрицата „ V “ от дясната страна на X_c = UΣV ' )
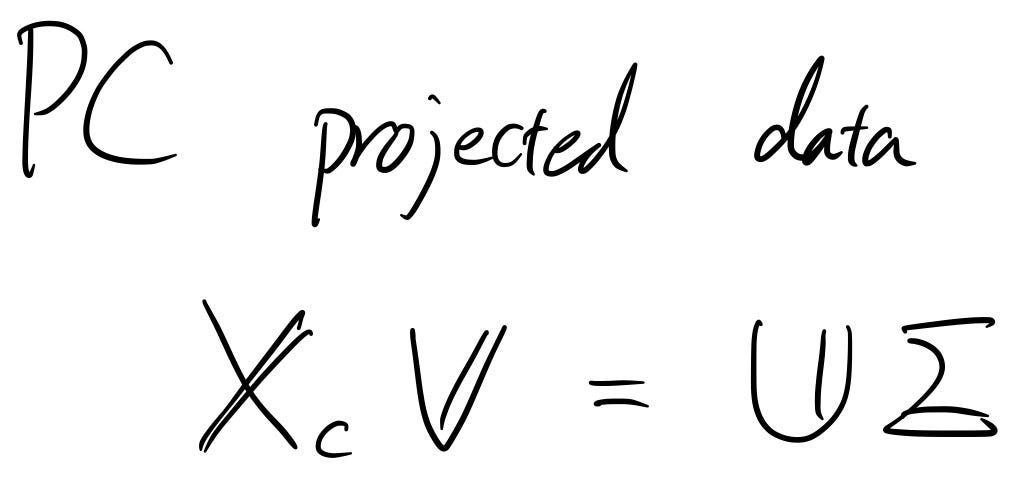
Обобщение
- PCA проектира данните върху основните компоненти, където дисперсията на данните е максимална (или общите разстояния от всяка точка до оста са минимизирани)
- Можете да изведете защо PCA е всичко за решаване на собственото разлагане на ковариационната матрица с помощта на множител на Лагранж
- На практика хората използват SVD за изчисляване на PCA поради ефективността на изчисленията
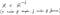
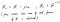
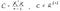
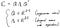
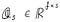
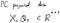
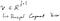
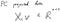
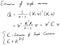
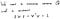
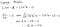
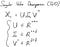
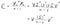
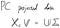
Няма коментари:
Публикуване на коментар